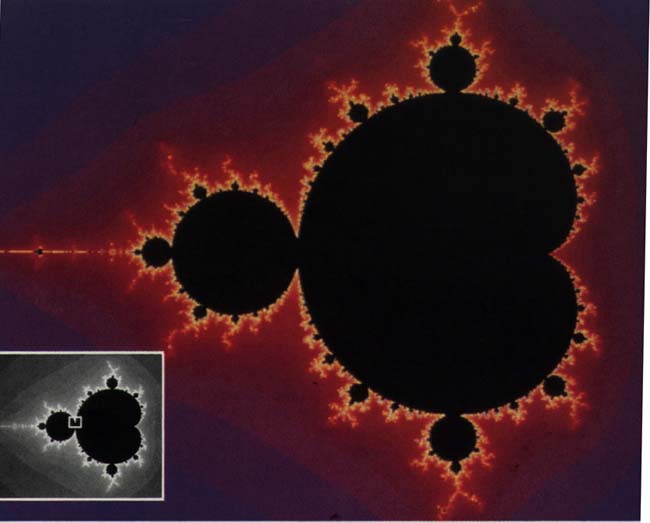
The Mandlebrot set has been described as the "most complicated object in the world." The figure represents the boundary of the domain of attraction of the behaviour of a simple equation in the complex plane. It is not the domain of attraction of a single system but rather a map of a family of systems, based on a single criterion.
Mandelbrot set
The complex plane consists of all numbers of the form z = a + bi, where a and b are real numbers and i is the square root of -1.
a series of complex numbers is constructed by the equation:
z subk = z sub k-1 squared + c, z sub0=0, k = 1,2,...
two different behaviours for this equation are observed, depending on the value of k. The sequence either goes off to infinity, wandering all over the complex plane, or the sequence remains bounded. for k=2, the former is the case, while for k=0 the latter holds true. The Mandlebrot set is the set of values for k in which the sequence remains bounded. It is the boundary between the two behaviours of the equation.
New copies of the entire Mandlebrot set continue to "bud off" from the origiinal at all scales of observation. Furthermore, new structures continue to appear as one goes to higher and higher magnifications. This never-ending sequence of new patterns has lead many to claim that the Mandlebrot set is the most complicated object known to mankind.
Furthermore, the Japanese mathematician Mitsuhiro Shishikura proved in 1991 that the dimension of the boundary of the Mandlebrot set is 2. Although the Mandlebrot set does not fill up the plane, (like the Peano curve) this measure of its "roughness" means that no curve can be more complex.